Variance represents the average of the squared deviations from the mean. Because we square the deviations, the variance is always a non-negative value, meaning it’s either positive or zero. The method for calculating variance slightly varies depending on whether we are dealing with a sample or a population.
Lets consider an hypothetical example of income, when we analyze income data, we discover that the sample variance is a large figure. Since this is a sample from a population, the sample variance is measured in thousands of rupees squared. This unit, rupees squared, can be challenging to interpret directly. Hence, we prefer using the standard deviation because it will be expressed in rupees, which provides a more intuitive understanding of the variability in the income data.
Key Takeaway
- The standard deviation represents the typical distance of observations from the mean.
- When the standard deviation is low, it suggests that most values cluster closely around the mean, indicating less variability.
- Conversely, a larger standard deviation implies greater variability, with values more spread out from the mean.
Standard Deviation: Population and Sample
When we discuss standard deviation, whether from a population or a sample, the formulas are essentially the same. We simply take the square root of the variance. In the case of population standard deviation, it’s the square root of population variance, and for sample standard deviation, it’s the square root of sample variances.
For our income data, calculating the sample standard deviation is straightforward using statistical software. Taking the square root of our sample variance gives us a standard deviation of approximately 55,000 rupees. This measurement is in the original units of rupees, unlike the sample variance, which is in rupees squared.
Conceptually, the standard deviation provides an indication of the typical distance of our income observations from the sample mean. On average, we can interpret this standard deviation to mean that incomes vary by about 55,000 rupees.
Standard Deviation Interpretation w.r.t Mean
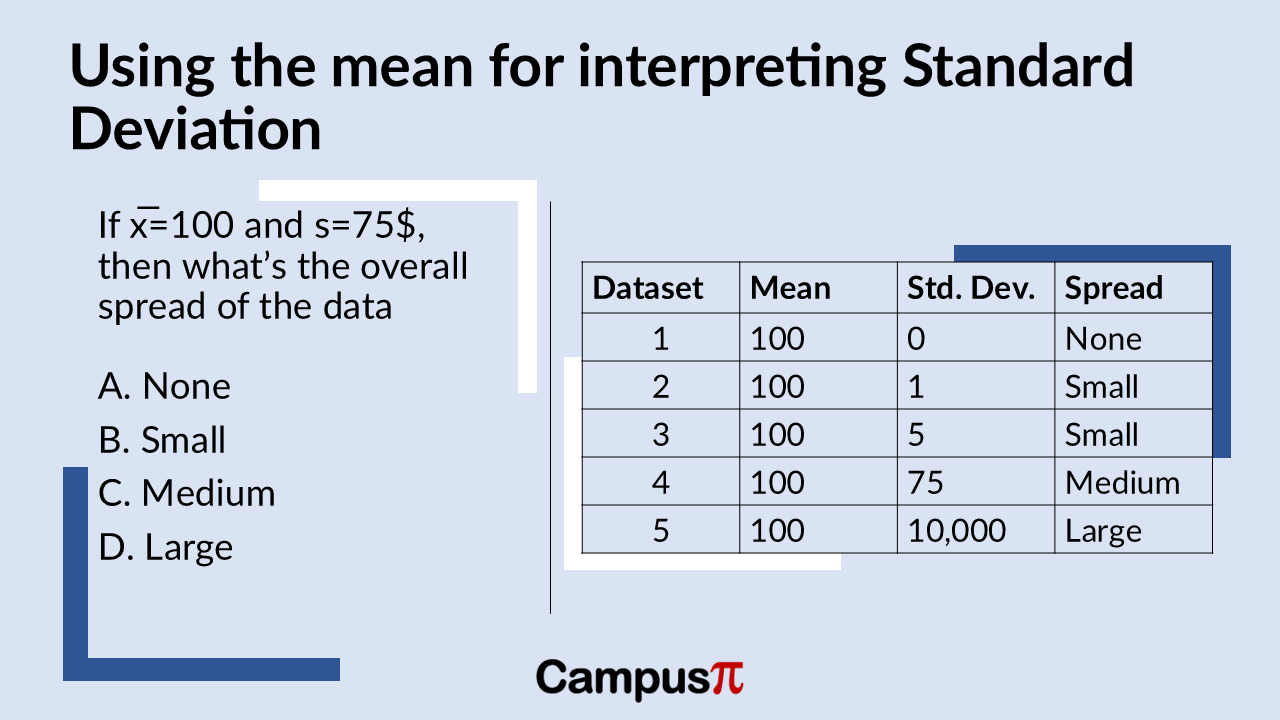
To better understand the standard deviation, especially in relation to income or any dataset, it’s helpful to consider its interpretation alongside the mean. The standard deviation represents the typical distance of observations from the mean.
For instance, if we have a dataset with a mean income of INR 100 and a sample standard deviation of INR 0, what does this tell us about the spread of the data? Well, with a standard deviation of zero, it means all values in the dataset are exactly 100. Therefore, the spread of the data in this case would be considered none.
This example illustrates how the mean can aid in interpreting the standard deviation. When the standard deviation is low, it suggests that most values cluster closely around the mean, indicating less variability. Conversely, a larger standard deviation implies greater variability, with values more spread out from the mean. This comparison helps provide a more intuitive understanding of what the standard deviation measures in a dataset.
If we have a sample standard deviation of one rupee and a sample mean of 100, it indicates that the data points are relatively close to the mean. The standard deviation being much smaller than the mean suggests that most observations cluster tightly around the mean value of 100. Therefore, the amount of variability or spread in the data is minimal in this case. A sample mean of 100 and a standard deviation of 5 and is still pretty small there’s not going to be very much variation around the data set.
Suppose our sample mean is 100 and the sample standard deviation is 75. In this case you can say the sample standard deviation is pretty close to the sample mean. So, let’s say that there’s just a medium amount of variability, you can think of it as there are quite a few observations around this sample mean but there is some degree of spread. Finally consider a mean of 100 and a standard deviation of ten thousand then the overall spread of the data it’s going to be large.
We can interpret the sample standard deviation by comparing it with the sample mean. In each scenario we’ve discussed, we’ve kept the sample mean consistent while varying the sample standard deviation.
When the sample standard deviation is significantly large compared to the sample mean, it indicates that the data points are widely spread around the mean. Conversely, if the sample standard deviation is relatively small compared to the sample mean, it suggests there is little variation, meaning most observations are closely clustered around the sample mean. Thus, comparing the standard deviation to the mean helps us gauge the degree of variability in the dataset.
Standard Deviation of Income
Let’s examine our income data to understand what the standard deviation is telling us. The sample standard deviation is 55,000, while the mean income is around 37,000. Since, the sample mean is smaller than the standard deviation, this indicates a relatively large spread around the mean. In other words, these values suggest a significant degree of variability in incomes based on this sample data.


